La relazione di Eulero afferma che in tutti i poliedri convessi F + V - S = 2. (http://upload.wikimedia.org/wikipedia/it/5/58/GeometriaSolida.gif)

Per cercare di afferrare la dimostrazione di Cauchy bisogna capire il significato di un termine della geometria moderna e cioè: topologia. La topologia è una delle più importanti branche della matematica moderna. Studia le proprietà delle figure che non cambiano quando viene effettuata una deformazione senza "strappi", "sovrapposizioni" o "incollature". Pensate di distorcere o deformare delle superfici senza bucarle o strapparle come se fossero fatte di gomma elastica. In questo modo si può capire quali siano le proprietà di una figura che resistono, per così dire, a queste deformazioni e restano quindi invarianti. Ciò che rimane invariato si chiama proprio invariante topologico.

Grafi poligonali utili per la dimostrazione della relazione di Eulero. (http://upload.wikimedia.org/wikipedia/it/1/17/DimEulero.jpg)

Per dimostrare la formula di Eulero, immaginiamo che il poliedro considerato sia cavo, con una superficie fatta di gomma sottile. Eulero notò che i cinque poliedri regolari dal punto di vista topologico non sono altro che grafi sulla sfera, cioè, immaginandoli di gomma e gonfiandoli, la loro superficie, se si toglie una faccia, si può deformare fino ad essere distesa sul piano. Seguite il ragionamento osservando la figura soprastante.
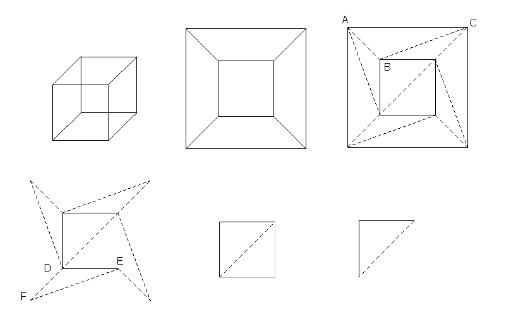
Ovviamente, le aree delle facce e gli angoli determinati dagli spigoli del poliedro verranno alterati dalla deformazione sul piano. Il reticolato piano dei vertici e degli spigoli, cioè la "nuova figura" piana, invece, conterrà lo stesso numero di vertici e di spigoli del poliedro originale, mentre il numero dei poligoni sarà diminuito di uno, perché è stata eliminata una faccia. Adesso seguendo la figura soprastante tracciamo una diagonale in un poligono della figura sul piano che non sia un triangolo. In questo modo aumentiamo di 1 sia F che S, mantenendo così inalterato il valore di V + F - S. Continuiamo a tracciare diagonali finché la figura risulta interamente formata da triangoli. Nella figura divisa in triangoli, V + F - S ha lo stesso valore che aveva prima, perché l’operazione di tracciare diagonali lo ha lasciato invariato, come abbiamo appena visto.
Consideriamo il triangolo ABC, che ha un lato sul contorno della figura e asportiamo quella parte di perimetro che non appartiene a nessun altro triangolo, cioè il lato AC e, con questo, anche la faccia da questo delimitata. Dal triangolo DEF asportiamo la faccia racchiusa, i due lati DF e FE e il vertice F. L’eliminazione di un triangolo del tipo ABC fa diminuire S ed F di 1 e lascia V inalterato, cosicché il valore di V + F - S rimane lo stesso. L’eliminazione di un triangolo del tipo DEF fa diminuire V di 1, S di 2, ed F di 1, cosicché il valore di V + F - S rimane ancora lo stesso. Con una opportuna successione di queste operazioni si possono eliminare i triangoli aventi dei lati sul contorno finché rimane un solo triangolo, con tre lati, tre vertici e una faccia. Per questo semplice triangolo, si ha che V + F - S = 3 + 1 - 3. Ma abbiamo visto che il valore di V + F - S rimane inalterato, perciò, anche nella figura originaria piana, V + F - S deve essere uguale a 1. Ne consegue che V + F - S è uguale a 1 nel poliedro deformato da cui è stata eliminata la faccia. Ma allora, nel poliedro originale, cioè aggiungendo la faccia tolta all'inizio, V + F - S = 2, che non è altro che la relazione di Eulero.
Ecco fatta la vostra prima dimostrazione topologica!!!

Ciao, Manuela (manuela_casasoli@yahoo.it).